[25NS] Luyện tập 01
Lập lịch Round-Robin
Nộp bàiCó \( n \) tiến trình trong một hàng đợi.
Mỗi tiến trình có \( \text{name}_i \) (tên) và \( \text{time}_i \) (thời gian thực thi).
Thuật toán Round-Robin scheduling xử lý các tiến trình theo thứ tự trong hàng đợi.
Bộ lập lịch Round-Robin cấp cho mỗi tiến trình một quantum (khoảng thời gian xử lý).
Nếu tiến trình chưa hoàn thành sau khoảng thời gian đó, nó sẽ bị tạm dừng, chuyển ra cuối hàng đợi, và bộ lập lịch sẽ xử lý tiến trình kế tiếp.
Giả sử ta có hàng đợi ban đầu với \( \text{quantum} = 100\,\text{ms} \):
\(A(150) - B(80) - C(200) - D(200)\)
Tiến trình A được xử lý trong 100 ms, sau đó bị tạm dừng và chuyển ra cuối hàng đợi với thời gian còn lại 50 ms:
\(B(80) - C(200) - D(200) - A(50)\)
Tiến trình B được xử lý trong 80 ms và hoàn thành tại thời điểm 180 ms, sau đó bị loại khỏi hàng đợi:
\(C(200) - D(200) - A(50)\)
Hãy viết một chương trình mô phỏng thuật toán round-robin scheduling.
Input
-
Dòng đầu chứa hai số nguyên: \( n \) và \( q \) — số lượng tiến trình và độ dài quantum (ms).
-
\( n \) dòng tiếp theo: Mỗi dòng chứa \( \text{name}_i \) và \( \text{time}_i \), trong đó:
- \( \text{name}_i \): tên của tiến trình
- \( \text{time}_i \): thời gian cần để hoàn thành (ms)
Output
In ra tên và thời gian hoàn thành của tiến trình theo thứ tự
Constraint
- \( 1 \le n \le 100000 \)
- \( 1 \le q \le 1000 \)
- \( 1 \le \text{time}_i \le 50000 \)
- \( 1 \le \text{length}(\text{name}_i) \le 10 \)
- \( 1 \le \sum \text{time}_i \le 1000000 \)
Test 1
Input
5 100
p1 150
p2 80
p3 200
p4 350
p5 20
Output
p2 180
p5 400
p1 450
p3 550
p4 800
Lập lịch Round-Robin (full)
Nộp bàiCó \(n\) tiến trình được xếp theo thứ tự trong một hàng đợi. Tiến trình thứ \(i\) có:
- \(\text{name}_i\): tên tiến trình
- \(\text{time}_i\): tổng thời gian CPU cần để hoàn thành (tính bằng ms)
Bộ lập lịch Round-Robin xử lý các tiến trình theo quy tắc:
- Luôn lấy tiến trình ở đầu hàng đợi để chạy.
- Cấp cho tiến trình đó tối đa \(q\) ms (quantum).
- Nếu tiến trình hoàn thành trong khoảng thời gian này, nó bị loại khỏi hàng đợi và ta ghi nhận thời điểm hoàn thành.
- Nếu tiến trình chưa hoàn thành, giảm thời gian còn lại đi \(q\) ms, sau đó đưa tiến trình xuống cuối hàng đợi.
Giả sử thời điểm bắt đầu là \(0\) ms và CPU luôn chạy liên tục khi hàng đợi còn tiến trình.
Ví dụ với \(q = 100\) và hàng đợi ban đầu:
\(A(150) - B(80) - C(200) - D(200)\)
- \(A\) chạy \(100\) ms, còn \(50\) ms → chuyển xuống cuối:
\(B(80) - C(200) - D(200) - A(50)\) - \(B\) chạy \(80\) ms và hoàn thành tại thời điểm \(180\) ms → bị loại khỏi hàng đợi.
Yêu cầu
Hãy mô phỏng Round-Robin và in ra tên cùng thời điểm hoàn thành của mỗi tiến trình theo đúng thứ tự hoàn thành.
Lưu ý (cải tiến): \(\text{time}_i\) có thể rất lớn, do đó lời giải mô phỏng từng lát \(q\) ms có thể không đủ nhanh.
Input
- Dòng đầu chứa hai số nguyên \(n\) và \(q\) — số lượng tiến trình và độ dài quantum (ms).
\(1 \le n \le 2 \cdot 10^5,\ 1 \le q \le 1000\) - \(n\) dòng tiếp theo, mỗi dòng chứa \(\text{name}_i\) và \(\text{time}_i\):
- \(\text{name}_i\): chuỗi không có khoảng trắng, độ dài từ \(1\) đến \(10\)
- \(\text{time}_i\): thời gian CPU cần để hoàn thành (ms)
\(1 \le \text{time}_i \le 10^{18}\)
Output
In ra \(n\) dòng, mỗi dòng gồm \(\text{name}_i\) và \(\text{finish}_i\) — tên tiến trình và thời điểm (ms) mà tiến trình đó hoàn thành.
Các dòng phải được in theo đúng thứ tự tiến trình hoàn thành.
📝 Ví dụ
Input:
5 100
p1 150
p2 80
p3 200
p4 350
p5 20
Output:
p2 180
p5 400
p1 450
p3 550
p4 800
🎯 Ràng buộc (Subtasks)
- Subtask 1 (20%): \(1 \le n \le 2000,\ 1 \le \text{time}_i \le 5 \cdot 10^4\)
- Subtask 2 (30%): \(1 \le n \le 10^5,\ \sum \text{time}_i \le 10^6\)
- Subtask 3 (50%): \(1 \le n \le 2 \cdot 10^5,\ 1 \le \text{time}_i \le 10^{18}\)
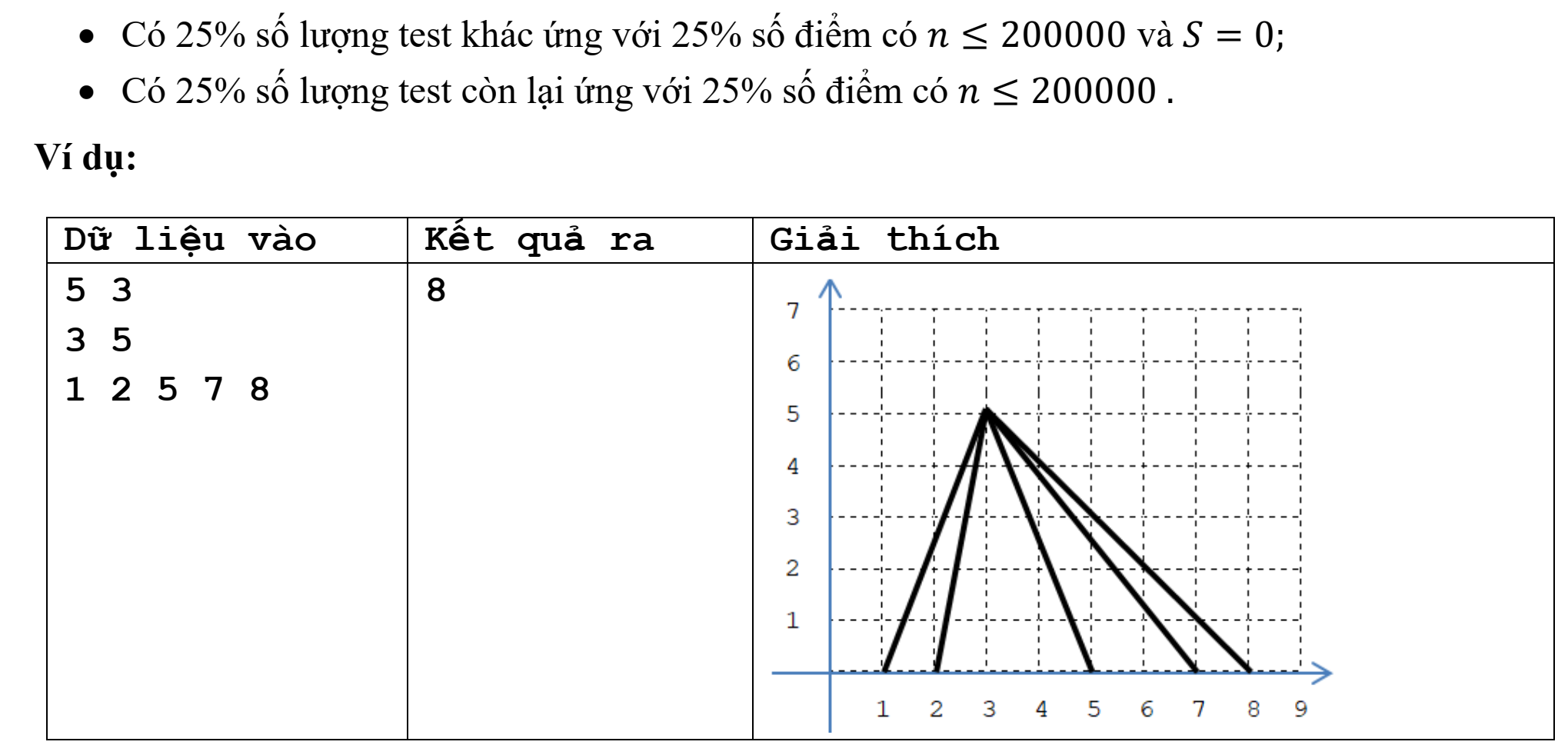
Trung vị tập hợp
Nộp bàiBạn có một tập hợp \(S\), ban đầu tập hợp này rỗng. Bạn cần thực hiện \(q\) truy vấn liên tiếp trên tập hợp này. Có hai loại truy vấn:
- Truy vấn loại 1 (
1 x): Kiểm tra xem số nguyên \(x\) có trong tập \(S\) hay không.- Nếu \(x\) chưa có trong \(S\), hãy thêm \(x\) vào \(S\).
- Nếu \(x\) đã có trong \(S\), hãy xóa \(x\) khỏi \(S\).
- Truy vấn loại 2 (
2): Tìm trung vị của tập hợp \(S\). Cách tìm như sau:- Sắp xếp các phần tử trong \(S\) theo thứ tự từ nhỏ đến lớn, đánh số thứ tự từ \(1\) đến \(n\) (\(n\) là số phần tử hiện tại).
- Nếu \(n\) là số lẻ, trung vị là phần tử đứng ở vị trí thứ \(\frac{n+1}{2}\).
- Nếu \(n\) là số chẵn, trung vị là trung bình cộng của hai phần tử đứng ở vị trí \(\frac{n}{2}\) và \(\frac{n}{2} + 1\).
- Đảm bảo rằng khi thực hiện truy vấn này, tập \(S\) luôn có ít nhất một phần tử.
Input
- Dòng đầu tiên chứa số nguyên \(q\) (\(1 \le q \le 10^5\)) là số lượng truy vấn.
- \(q\) dòng tiếp theo, mỗi dòng chứa một truy vấn theo định dạng:
1 x: Với \(x\) là số nguyên dương (\(1 \le x \le 10^9\)).2: Yêu cầu tìm trung vị.
Output
- Với mỗi truy vấn loại 2, in ra kết quả trên một dòng.
- Nếu kết quả là số thập phân, hãy làm tròn và in ra đúng một chữ số sau dấu phẩy.
Examples
Test 1
Input
6
1 5
1 10
2
1 20
2
1 5Output
7.5
10Explanation
- Ban đầu \(S = \emptyset\).
1 5: Thêm 5. \(S = \{5\}\).1 10: Thêm 10. \(S = \{5, 10\}\).2: \(n=2\) (chẵn). Các phần tử là 5 và 10. Trung vị = \((5+10)/2 = 7.5\).1 20: Thêm 20. \(S = \{5, 10, 20\}\).2: \(n=3\) (lẻ). Phần tử ở giữa (vị trí thứ 2) là 10. In ra 10.0.1 5: Xóa 5 (vì 5 đã có). \(S = \{10, 20\}\).
Test 2
Input
5
1 2
1 2
1 100
1 200
2Output
150Explanation
1 2: Thêm 2. \(S = \{2\}\).1 2: Xóa 2. \(S = \emptyset\).1 100: Thêm 100. \(S = \{100\}\).1 200: Thêm 200. \(S = \{100, 200\}\).2: \(n=2\). Trung vị = \((100+200)/2 = 150.0\).
Scoring
- Subtask \(1\) (\(30\%\) số điểm): \(q \le 1000\).
- Subtask \(2\) (\(70\%\) số điểm): Không có ràng buộc gì thêm (theo global constraint).
Dãy cấp số nhân
Nộp bàiBài 1: Dãy cấp số nhân
Tổng bình phương
Nộp bàiCho mảng \(A\) gồm \(N\) số nguyên dương.
Hãy tính tổng bình phương của tổng tất cả các dãy con liên tiếp của mảng \(A\).
Cụ thể, gọi \(sum(l, r)\) là tổng các phần tử từ vị trí \(l\) đến \(r\) (\(1 \le l \le r \le N\)).
Ta cần tính giá trị:
Do kết quả có thể rất lớn, hãy in ra kết quả lấy modulo \(10^9 + 7\).
Input
- Dòng đầu tiên chứa số nguyên \(N\) (\(1 \le N \le 300000\)).
- Dòng thứ hai chứa \(N\) số nguyên dương \(A[i]\) (\(A[i] \le 10^9\)).
Output
- In ra một số nguyên duy nhất, là giá trị cần tìm modulo \(10^9 + 7\).
Examples
Test 1
Input
3
3 2 4Output
171Explanation
Các dãy con liên tiếp và tổng của chúng:
- \([3] \rightarrow 3^2 = 9\)
- \([3,2] \rightarrow 5^2 = 25\)
- \([3,2,4] \rightarrow 9^2 = 81\)
- \([2] \rightarrow 2^2 = 4\)
- \([2,4] \rightarrow 6^2 = 36\)
- \([4] \rightarrow 4^2 = 16\)
Tổng tất cả là \(9 + 25 + 81 + 4 + 36 + 16 = 171\).
Scoring
- Subtask 1 (50% số điểm): \(N \le 5000\).
- Subtask 2 (50% số điểm): \(N \le 300000\).
Tìm vị trí
Nộp bàiCho \(N\) điểm (tương đương \(N\) cây xanh) nằm trên trục \(Ox\), các điểm được đánh số từ \(1\) đến \(N\).
Vị trí ban đầu của điểm thứ \(i\) là \(x[i]\).
Có \(M\) thao tác, thao tác thứ \(j\) cho một số nguyên \(k_j\) và đối xứng tất cả các điểm qua đường thẳng \(x = k_j\).
Nói cách khác, sau thao tác này, mọi điểm ở vị trí \(x\) sẽ chuyển thành \(x' = 2k_j - x\).
Có \(Q\) truy vấn, mỗi truy vấn gồm hai số nguyên \((id, K)\):
Hãy in ra vị trí của điểm thứ \(id\) sau khi thực hiện \(K\) thao tác đầu tiên.
Input
- Dòng đầu tiên chứa ba số nguyên \(N, M, Q\).
- Dòng thứ hai chứa \(N\) số nguyên \(x[1], x[2], \dots, x[N]\) (vị trí ban đầu của các điểm), với \(|x[i]| \le 10^9\).
- \(M\) dòng tiếp theo, dòng thứ \(j\) chứa một số nguyên \(k_j\) (mô tả thao tác đối xứng qua \(x = k_j\)).
- \(Q\) dòng tiếp theo, mỗi dòng gồm hai số nguyên \(id, K\) \((1 \le id \le N,\ 0 \le K \le M)\).
Output
- In ra \(Q\) dòng, mỗi dòng là đáp án của truy vấn tương ứng.
Examples
Test 1
Input
4 3 5
3 2 -1 -4
2
4
1
2 1
2 2
2 3
4 1
3 2Output
2
6
-4
8
3Explanation
Sau thao tác 1 (đối xứng qua \(x=2\)): vị trí trở thành \(1\ 2\ 5\ 8\).
Sau thao tác 2 (đối xứng qua \(x=4\)): vị trí trở thành \(7\ 6\ 3\ 0\).
Sau thao tác 3 (đối xứng qua \(x=1\)): vị trí trở thành \(-5\ -4\ -1\ 2\).
Ví dụ truy vấn \((2,3)\) hỏi vị trí điểm 2 sau 3 thao tác, kết quả là \(-4\).
Scoring
- Subtask 1 (50% số điểm): \(N, M, Q \le 1000\).
- Subtask 2 (50% số điểm): \(N, M, Q \le 300000\).